Начнём с того, что расширим наше понимание слайда. Примером нам послужит вот это место на карте kzpl_desert_wellspring:


Запрыгнув в левый стык в приседе, мы можем прослайдить разлом, не теряя скорость. Как это возможно? В статье про физику Edgebug и JumpBug мы разбирали работу функции PM_CategorizePosition, которая с помощью PM_PlayerTrace проверяла, насколько сильно наклонена плоскость под игроком, и в зависимости от наклона выставляла флаг onground. Но что если касание происходит сразу с двумя плоскостями? Как мы выяснили из статьи про физику Pixelwalk, PM_PlayerTrace может находить разную плоскость в зависимости от того, в каком порядке плоскости записаны в bsp-девере. Получается, что если одна из плоскостей имеет наклон слайда, а вторая нет, то один и тот же стык плоскостей будет определяться движком либо как слайд, либо как земля, в зависимости от работы компилятора карты. Мало того, поскольку bsp-деревья для стоячей и сидячей моделек отличаются, то в одном месте может быть возможно слайдить только сидя или только стоя, а иногда работают оба варианта.

Теперь разберёмся, что происходит на стыке двух плоскостей с нашей скоростью. Мы уже смотрели на то, как PM_FlyMove проецирует вектор скорости при последовательном его пересечении нескольких плоскостей. При этом подразумевалось, что после столкновения с каждой плоскостью игрок перемещается вдоль неё на ненулевое расстояние. Однако если такое перемещение невозможно, то PM_FlyMove увеличивает счётчик плоскостей numplanes, после чего запускает обработку одновременного пересечения плоскостей. В прошлом мы намеренно опустили этот код, чтобы не усложнять статью, но сейчас настало время взглянуть на пропущенный кусочек:


В случае с нашим стыком этот код спроецирует вектор скорости сначала на одну плоскость, затем на другую, а вот дальше всё будет зависеть от угла между плоскостями. Если он меньше 90°, то скалярное произведение DotProduct вектора скорости velocity и нормали к плоскости planes[j] на каждом шаге цикла будет отрицательно:


Это значит, что j не достигнет значения numplanes, а вот i достигнет, и мы попадём в следующую часть кода. В ней вычисляется величина проекции вектора скорости на направление, параллельное обеим плоскостям, после чего итоговый вектор масштабируется до этой величины. Следовательно, что чем большая часть скорости осталась после проецирования её на плоскости (то есть чем меньше угол между плоскостями), тем быстрее будет уменьшаться часть скорости, параллельная плоскостям. Такой эффект торможения знаком каждому, кто попадал в стык между двумя слайдами.

Особенным является случай, когда между плоскостями ровно 90°. Тогда после проецирования на плоскости от вектора скорости остаётся только горизонтальная составляющая, перпендикулярная обеим нормалям, а значит скалярное произведение с этими нормалями будет нулевым, j достигнет значения numplanes, и далее скорость уже меняться не будет. Именно такой случай мы наблюдаем на kzpl_desert_wellspring, где при движении по стыку горизонтальная скорость не теряется (а при задействовании клавиши стрейфа может ещё и увеличиться).


Вообще говоря, мы уже сталкивались с очень похожей на WallBug техникой в конце статьи про физику Cliptype. Там речь шла про первый прыжок на holy_lame, для которого нам пришлось прорваться сквозь барьер толщиной в 0.03125 юнита между моделькой и плоскостью браша. Для этого в прыжке нужно было присесть и, смотря в сторону блока, зажать W и D (либо W и A). Благодаря работе PM_AirAccelerate скорость в направлении браша оказывалась настолько маленькой, что конец её вектора не пересекал плоскость браша, и это позволяло нам придвинуться к блоку поближе. Собственно ровно тот же принцип работает и для WallBug, разве что выполняется эта техника обычно спиной к стене (хотя с таким же успехом можно выполнять WallBug и лицом, и боком к стене, меняется только комбинация клавиш). Остаётся только понять, почему в какой-то момент сближения со стеной происходит обнуление скорости.

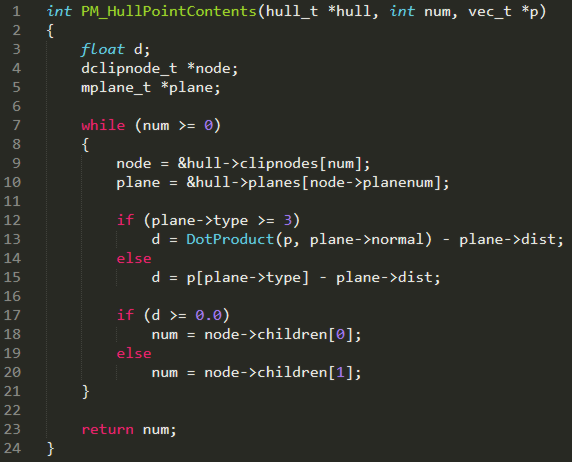
По идее после PM_AirAccelerate рассчитанный вектор скорости должен быть спроецирован на плоскость браша в PM_FlyMove, после чего на следующем шаге цикла трейс в PM_PlayerTrace уже ничего не задевает, и падение должно продолжиться. Однако если мы оказались слишком близко к стене, то функция PM_HullPointContents из PM_PlayerTrace, проверяющая, не находится ли точка трейса внутри браша, может сработать некорретно. Посмотрим что именно она делает:


Как видим, она пробегается по дереву браша и по ходу определяет величину d, по модулю равную расстоянию от заданной точки до соответствующей плоскости, при этом знак d указывает, по какую сторону от плоскости находится точка. Тип плоскости plane->type определяет ориентацию её нормали. Типы от 0 до 2 – это плоскости с нормалями, параллельными осям X, Y, Z, для них d определяется предельно просто. А вот для остальных плоскостей расчёт использует скалярное произведение DotProduct, и тут происходит классическая ошибка программиста при работе с математической функцией. Дело в том, что математически тут всё написано совершенно верно, однако из-за того, что тип float имеет вполне конечную точность, при работе с переменными, заданными во float, накапливается погрешность (особенно при умножении), и любые сравнения нужно проводить с учётом этой погрешности. По идее отступ 0.03125 от стены должен спасать от этих заморочек, однако реализация PM_PlayerTrace позволила нам преодолеть этот отступ.

Итак, вот что мы получаем в итоге. Расчёт d даёт неправильный знак, PM_HullPointContents утверждает, что мы оказались внутри браша, PM_PlayerTrace возвращает fraction = 0.0, в PM_FlyMove на следующих итерациях цикла мы получаем столкновения всё с той же плоскостью. В итоге либо мы дойдём до кода, который мы только что наблюдали при разборе слайда на стыке, и там векторное произведение CrossProduct нормали на саму себя даст ноль, на который затем умножится вектор скорости, либо после четырёх итераций цикла трейс так и не даст нам продвинуться, суммарный allFraction останется нулевым, и скорость опять же обнулится.

Получается, что любая плоскость, не параллельная базисным направлениям, может стать причиной внезапного застревания. И если держаться подальше от стенок возможность зачастую есть, то вот на слайдах от таких застреваний никуда не деться.


На этом цикл статей по физике игры завершается. Когда начинал писать, то не ожидал, что это зайдёт так далеко :) Изначально я хотел поделиться знаниями о работе стрейфов и bhop'а, но по ходу добавлялось всё больше техник, и каждая из них, казалось бы уже давно всем известная, открывала что-то новое и интересное. Когда я разобрался с тем, как устроен pixelwalk, я понял что нужно будет делать ещё несколько подготовительных частей, и то что я узнал уже по ходу их создания, оказалось действительно впечатляющим. Подобно тому, как физики изучают природу и предсказывают явления, мы погрузились в изучение творения самих людей, и это было не менее увлекательно.